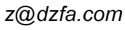傅立叶变换 - 傅里叶变换公式
傅里叶变换是一种将信号从时域转换到频域的数学工具,它揭示了所有满足一定条件的波形都可以表示为多个不同频率的正弦波叠加。🔍 拆解说明:
“所有的波” → 更精确说法是:所有满足条件的函数(例如有限能量的信号)“多个正弦波叠加” → 实际上是不同频率、幅度和相位的正弦波组成“傅里叶变换是一种变换规则” → 即是一种时域 ↔ 频域之间的映射📘 学术的表达【傅里叶变换公式(连续时间)】:对于满足狄里赫雷条件(Dirichlet conditions)的信号 f(t),傅里叶变换提供了将其分解为正弦波频率分量的方式,即:
这里, 𝐹 ( 𝜔 )就是在频域中,信号的各频率成分。
各个符号的含义
符号名称含义
F(ω)
频域函数输入信号 f(t)在频率 ω上的复数幅度,描述该频率在信号中占的“多少”和“相位”
ω
角频率(rad/s)单位为弧度每秒:ω=2πf,其中 f是普通频率(Hz)
f(t)
时域函数原始信号,在时间 t 上的幅度
t
时间变量自变量,单位为秒
复指数函数代表一个频率为 ω的复正弦波,用于“扫描”信号的频率成分
j
虚数单位j^2 = -1,电路中用 j表示虚数(而不是数学中的 i)
积分符号表示将整个时间轴上的信号投影到频率 ω上,提取该频率的成分
傅里叶变换把复杂的波,拆成简单的频率拼图,揭示了信号背后的“频率DNA”。
什么样的信号可以做傅里叶级数展开?
也就是——满足狄里赫雷条件(Dirichlet conditions)的信号 f(t)是什么样的?
📜 正式定义:狄里赫雷条件(Dirichlet Conditions)设 f(t)是一个在区间 上定义的函数,要使得它可以表示为一个傅里叶级数(Fourier Series),它必须满足以下三条条件:
1. 在有限区间内绝对可积
意思是:信号的“面积”不能是无穷大,不能炸掉。
2. 在一个周期内只有有限个极值(峰谷)
[*]函数不能无限震荡
[*]类似“锯齿”“方波”这类“有拐角”但可数的跳跃是可以接受的
3. 在一个周期内只有有限个间断点(不连续)
[*]可以有跳跃,例如方波
[*]不能是到处都断裂、不可预测的乱跳(如狄拉克函数就不满足)
🟢 常见满足狄里赫雷条件的信号示例:
信号是否满足说明
正弦波、余弦波✅连续光滑,当然满足
方波(周期性)✅有跳跃但可数
锯齿波✅有角但连续
三角波✅光滑的角
有限段定义的函数(如脉冲串)✅若幅度有限、断点有限即可
随机跳变函数❌如果无限不连续,就不满足
狄拉克δ函数❌是广义函数,不满足严格定义的可积性
🧠 直觉总结:
条件类比
面积有限函数不能“炸”
峰谷有限函数不能“抖成狗”
跳跃有限函数不能“抽风”
🚨 注意:
[*]这些条件是傅里叶级数展开的要求(用于周期信号);
[*]如果是要做傅里叶变换(处理非周期信号),则更强的一般要求是:
✅ 一句话超级通俗解释:所有的声音、图像、信号,其实都可以看作是「很多不同频率的正弦波」组合而成的。傅里叶级数是「重复的信号」拆解成「固定频率」的波;傅里叶变换是「不重复的信号」拆成「所有可能频率」的波。
📦 打个比方:你在听音乐假设你听一段音乐,这段音乐是个复杂的声音波形:
[*]有低音(低频正弦波)
[*]有高音(高频正弦波)
[*]有节奏重复(周期性)或者变化(非周期性)
你耳朵其实就是把整个声音波形拆解成一个个不同频率的音来听的。傅里叶理论就是用数学方式,把这件事精确地做出来。
页:
[1]