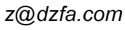傅里叶级数展开的奇函数形式
如何用一组正弦波叠加近似还原出一个方波(或类似方波的函数)这是一个傅里叶级数展开的奇函数形式,用来逼近方波、矩形波等“非光滑”函数。每一项都是一个频率不同的正弦波。
📘 每一项解释:
[*]sin[(2n−1)x]:是奇次谐波(1、3、5、7...)
[*]:是幅度衰减因子,频率越高,振幅越小
[*]总体是:“频率越高的正弦波贡献越小”
🧠 总结一句话:图中公式展示了 “复杂信号 = 不同频率的正弦波相加” 的思想,是傅里叶级数的直观演示,说明再不规则的波,也能用光滑的正弦波还原。 ✅ 一句话超级通俗解释:所有的声音、图像、信号,其实都可以看作是「很多不同频率的正弦波」组合而成的。傅里叶级数是「重复的信号」拆解成「固定频率」的波;傅里叶变换是「不重复的信号」拆成「所有可能频率」的波。
📦 打个比方:你在听音乐假设你听一段音乐,这段音乐是个复杂的声音波形:
[*]有低音(低频正弦波)
[*]有高音(高频正弦波)
[*]有节奏重复(周期性)或者变化(非周期性)
你耳朵其实就是把整个声音波形拆解成一个个不同频率的音来听的。傅里叶理论就是用数学方式,把这件事精确地做出来。
页:
[1]