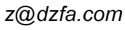傅里叶级数(Fourier Series)、傅里叶变换(Fourier Transform)对比
✅ 一、图中公式(傅里叶级数的一个特例)✳️ 本质:这是一个 傅里叶级数(Fourier Series),专门用于周期函数的频谱展开(如方波、锯齿波、三角波等)。
这里我们看到的是一个奇函数的正弦展开,专用于周期为 2π 的方波近似:
这是所谓的“方波”傅里叶展开,公式中只保留了奇次正弦波成分。
✅ 二、傅里叶变换公式(通用非周期信号)
✳️ 本质:傅里叶变换适用于非周期函数或任意有限能量信号,将其变换为连续频率谱。
[*]输入是任意函数 f(t)
[*]输出是频域函数 F(ω),表示“频率成分的多少”
[*]用于语音、图像、雷达、无线电等信号处理领域
🔍 关键区别对比表:
对比项傅里叶级数(Fourier Series)傅里叶变换(Fourier Transform)
适用对象周期函数非周期函数或有限能量信号
输出结果一组离散频率分量(谐波)一个连续频率谱
常见形式正弦、余弦展开复指数形式 e−jωt
典型应用分析方波、音调合成等分析语音、雷达、图像等非周期信号
数学表达级数相加 ∑积分 ∫
单位周期示例
🧠 形象总结:
类比方式傅里叶级数傅里叶变换
像什么?像拼图,用几块积木拼一个周期图案像调频收音机,扫描所有频率看哪段最强
拆解方式拆成固定频率的谐波(整数倍)拆成任意频率的连续成分
频率轴离散点(1Hz、2Hz、3Hz...)连续轴(0Hz 到 ∞Hz)
✅ 一句话超级通俗解释:所有的声音、图像、信号,其实都可以看作是「很多不同频率的正弦波」组合而成的。傅里叶级数是「重复的信号」拆解成「固定频率」的波;傅里叶变换是「不重复的信号」拆成「所有可能频率」的波。
📦 打个比方:你在听音乐假设你听一段音乐,这段音乐是个复杂的声音波形:
[*]有低音(低频正弦波)
[*]有高音(高频正弦波)
[*]有节奏重复(周期性)或者变化(非周期性)
你耳朵其实就是把整个声音波形拆解成一个个不同频率的音来听的。傅里叶理论就是用数学方式,把这件事精确地做出来。
页:
[1]